Cyberlog.eu

Pour une Bretagne libre...

Accueil > Recherche et développement > Stéréovision > Stéréovision par projection sur un plan virtuel (Bernard Couapel)

Stéréovision par projection sur un plan virtuel (Bernard Couapel)

samedi 2 février 2013, par bc

Toutes les versions de cet article : [English] [français]

Notre technique s’inscrit dans les approches
géométriques avec pour originalité le fait de
nécessiter des calculs en majeure partie bidimensionnels. Nous
utilisons un Plan Virtuel Intermédiaire Virtuel (VIP) qui est
défini par trois points supposés connus de la
scène. Nous obtenons une disparité entre points
homologues par une double projection du point de l’image homologue
sur l’image de référence en passant par le VIP. Cette
disparité est fonction de la distance du point à la
caméra et de son altitude par rapport au VIP.

Stéréovision par projection sur un plan virtuel

Stéréovision par projection sur un Plan Virtuel

Bernard COUAPEL
Version PDF

Abstract
1. Introduction
2. Notations et présentation générale
3. Double projection et géométrie épipolaire
- 3.1 Résolution
- 3.2 Résultats
4. Projection sur le VIP et calcul de C et C'
5. Conclusion
Remerciements
Bibliographie

Abstract

This paper presents a geometrical method to calculate the position of points in 3D space from two different views. Our method is divided in two steps. The first step is two-dimensional and defines the epipolar geometry. It calculates a double projection of the homologous image on the reference image through a Virtual Intermediate Plane. We use eight corresponding points to calculate the transformation of the homologous image. The disparity between the corresponding points in a same referential allows us to get some information about the position of the 3D points. The second step calculates the coordinates of points in a projective space. The calculation of 3D coordinates consists in a simple transformation of projective to cartesian coordinates with 5 points in the case of a pinhole camera, and 4 points for the parallel projection. The interest of our method is to calculate the relative positionning without any knowledge on 3D coordinates of points, to offer controls along the calculation and to postpone use of the reference points at the end of the calculation.
Keywords: stereovision, geometry, calibration, relative positionning

1. Introduction

Un des principaux sujets de recherche en vision par ordinateur porte sur la stéréovision, c'est à dire le calcul de points dans l'espace, à partir de leurs images prises de différentes positions par une caméra de type sténopé. La première approche de ce problème consiste à calibrer le système de prise de vues stéréoscopiques, c'est à dire de calculer les paramètres intrinsèques des caméras et leur positionnement relatif. Des travaux dans ce domaine sont présentés dans [CHAU89] and [HONG91]. C'est aussi la méthode de calcul utilisée en photogrammétrie depuis de nombreuses années [CARR71] [HURA60]. Une nouvelle approche du problème est issue des travaux de [LONG81] qui a présenté une méthode permettant de calculer la géométrie épipolaire induite par le modèle sténopé. Ces travaux ont été étendus à l'espace par des méthodes algébriques qui calculent les matrices de transformation des caméras à l'aide de cinq points de la scène [FAUG92] [LUON92], et des méthodes géométriques qui utilisent deux ensembles de quatre points coplanaires de la scène [MORI93] [MOHR92]. Récemment, [SHAS93] a proposé une méthode de reconstruction qui utilise quatre points de la scène définissant un tétraèdre ainsi que le centre de projection de la caméra comme cinquième point de référence. L'auteur calcule un invariant projectif et définit un nouvel élément descriptif: la distance projective (projective depth).
Notre technique s'inscrit dans les approches géométriques avec pour originalité le fait de nécessiter des calculs en majeure partie bidimensionnels. Nous utilisons un Plan Virtuel Intermédiaire Virtuel (VIP) qui est défini par trois points supposés connus de la scène. Nous obtenons une disparité entre points homologues par une double projection du point de l'image homologue sur l'image de référence en passant par le VIP. Cette disparité est fonction de la distance du point à la caméra et de son altitude par rapport au VIP.

La première étape de notre méthode est décrite dans le chapitre 3 de cet article. Elle permet de calculer l'épipôle et le recalcul de l'image homologue par rapport à l'image de référence à l'aide de 8 couples de points appariés sur les deux images. La seconde étape décrite dans le chapitre 4 calcule de positionnement relatif des points dans un espace projectif défini par cinq points de la scène supposés connus. Les coordonnées cartésiennes sont obtenues à la fin de l'algorithme par un simple changement de repère projectif - cartésien, en utilisant les coordonnées de cinq points de la scène dans le cas du modèle sténopé, et quatre points pour la projection parallèle.

Notre méthode a pour avantages d'offrir des autocontrôles sur la validité des appariements de points, et aussi le fait que le recalcul de l'image homologue donne des informations directement interprétables sur le positionnement des points dans l'espace. Cette transformation de l'image homologue est d'autre part très utile pour la mise en correspondance des deux images, puisque les images des points 3D appartenant au VIP sont directement mis en correspondance.

2. Notations et présentation générale

Pour décrire notre méthode de calcul, nous utiliserons les notations suivantes.
Les coordonnées cartésiennes sont notées en minuscules et les coordonnées projectives en majuscules. Pour chaque point décrit ci-dessous, nous donnons les coordonnées cartésiennes et projectives correspondantes.
Nous utilisons deux caméras S et S', et l'homologue d'un élément x de S est noté x' sur S'.
Pour la caméra S, le plan image est noté Q, le centre de projection: C (xc,yc,zc) ou (Xc,Yc,Zc,Tc), l'épipôle: E (xe,ye) ou (Xe,Ye,Ze), et les points images: Mi (xi,yi) ou (Xi,Yi,Zi).
Les points 3D sont notés Pi (xi*,yi*,zi*) ou (Xi*,Yi*,Zi*,Ti*).
Nous utilisons un Plan Virtuel dans l'espace, noté VIP. Les points sur le VIP sont notés en minuscule.
Les deux homographies correspondant aux projections de Q sur VIP par C et Q' sur VIP par C' sont notées respectivement H1 et H2.
Le recalcul d'un point Mi' de Q' sur Q après double projection par le VIP est noté Mi" (xi",yi") ou (Xi",Yi",Zi").

Notre méthode s'appuie sur deux images stéréoscopiques. L'une est appelée image de référence et reste inchangée pendant les calculs. Elle correspond au plan image Q de la caméra S. La seconde est appelée image homologue. Elle est transformée pendant les calculs et correspond au plan image Q' de la caméra S'.

2.1 Géométrie épipolaire

Dans les figures qui suivent, nous prenons comme convention que le centre de projection se trouve en avant du plan image, ce qui diffère des représentations habituelles.
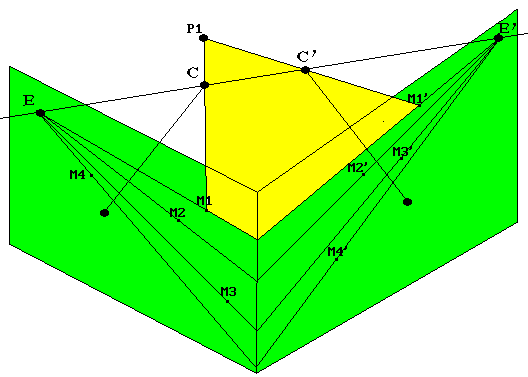
Les relations entre les points dans l'espace et leurs images sur les plans de projection sont présentées Fig1. Les cinq points P1,C,C',M1 and M1' sont coplanaires et définissent la géométrie épipolaire [LONG81] qui décrit deux faisceaux de droites homologues se coupant à l'intersection des deux plans images dans l'espace. Les droites homologues sont appelées droites épipolaires homologues et les centres de ces faisceaux épipôles. Les épipôles sont définis par l'intersection de la droite passant par les centres de projection et les plans images. Cette géométrie induit des contraintes que nous utilisons au cours de cette présentation.

Fig.1: Géometrie épipolaire

2.2 Cas de stéréovision simplifié

La figure 2 présente un cas simplifié de stéréovision dans lequel les deux plans de projection sont confondus avec un plan de l'espace défini par trois points (non alignés). Dans ce cas, il n'y a qu'un seul épipôle e.

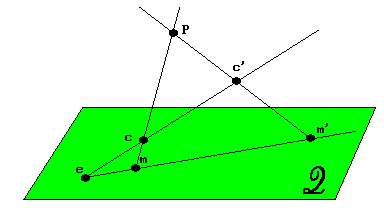
Fig.2: Cas simplifié de stéréovision

Le calcul d'un point P est facilement obtenu par l'intersection des droites {C,M} et {C',M'} dans l'espace.
Si les positions de C et C' sont inconnues, il est possible de les calculer si l'on connaît les positions de deux points P1 et P2 ainsi que leurs images (M1,M1') (M2,M2') sur Q. C est obtenu par l'intersection de {P1,M1} et {P2,M2}, et C' par l'intersection de {P1,M1'} et {P2,M2'}. Nous avons au total utilisé trois points pour définir Q et deux points pour calculer les centres de projection.
Notre but est de ramener le cas général de stéréovision à ce cas particulier.

2.3 Cas général de stéréovision

Le cas général de stéréovision est présenté figure 3. Nous ne savons pas où sont situés les deux plans de projection dans l'espace, mais le modèle sténopé induit une géométrie épipolaire, et la coplanarité de tous les points représentés sur la figure 3.
Nous ramenons ce cas général de stéréovision au cas particulier présenté au paragraphe précédent en utilisant un Plan Intermédiaire Virtuel (VIP) dans l'espace.

Fig.3: Cas général de stéréovision

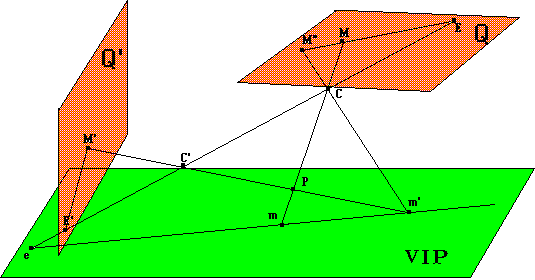
Notre méthode de calcul est divisée en deux étapes:

La première partie détermine la géométrie épipolaire en s'appuyant sur l'homographie H liant bijectivement les plans images par les deux projections qui s'appuient sur le plan virtuel. H est la composition de la projection H2 de Q' par C' sur le VIP et de la projection H1 du VIP sur Q par C. H est telle que pour un point P du VIP, M"=H(M') est confondu avec M sur Q. En revanche, si ce point n'est pas sur le VIP, alors la droite {M,M"} intersecte l'épipôle E sur Q. La définition de H est obtenue avec huit couples de points homologues sur Q et Q'.

La seconde étape consiste à projeter Q et H(Q') sur le VIP et à calculer la position de C et C' dans l'espace. Ceci nous ramène alors au cas particulier présenté au début de ce chapitre. Les calculs nécessitent la connaissance de cinq points non coplanaires de l'espace ainsi que leurs images, mais si on considère ces points comme base d'un espace projectif il est possible de calculer les points de la scène dans cet espace et obtenir ainsi leur positionnement relatif sans utiliser d'information 3D. On se ramène ainsi aux solutions proposées par Faugeras, Hartley et Mohr.

3. Double projection et géométrie épipolaire

Le projection H1 de Q sur VIP par C et la projection H2 de Q' sur VIP par C' correspondent à des homographies de plan à plan.

Propriétés des homographies [EFIM81]:
- un homographie non dégénérée est une application bijective définie par une matrice inversible.
- les homographies forment un groupe, donc une composition d'homographies, ou l'inverse d'une homographie est aussi une homographie.
- une homographie conserve le birapport de quatre points alignés.
Nous calculons la composition H des projections H2 et H1-1 qui transforment les points Mi' dans Q' en points Mi" sur Q. Cette double projection est une homographie avec les propriétés suivantes:

1) Pour les points Pi qui appartiennent au VIP, les transformés Mi"=H(Mi') sur Q des images Mi' sur Q' sont confondus avec les points Mi sur Q.

2) Pour les points Pi qui n'appartiennent par au VIP, le transformé Mi"=H(Mi') est aligné avec la droite {Mi,E} sur Q.

3.1 Résolution

Les projections des trois points définissant le VIP sont choisis comme les trois premiers points (M1,M2,M3 / M1',M2',M3') de la base projective de chaque image (a qui il faut ajouter un quatrième point pour compléter la base). Chacun de ces triplets est appelé triplet des points de base. On leur affecte respectivement les coordonnées homogènes (0,0,1), (0,1,0), (1,0,0). Si nous choisissons comme point unitaire (1,1,1) de la base projective le barycentre de ces trois points, alors les coordonnées cartésiennes (xi,yi) sur Q sont transformées en coordonnées projectives (Xi,Yi,Zi) par la matrice:

|Xi| |x1 x2 x3|^-1 |xi|
|Yi|=|y1 y2 y3| * |yi|
|Zi| |.1 .1 .1| . | 1|

Tranformation en coordonnées projectives

Nous construisons une matrice similaire pour Q' avec les coordonnées des points homologues.

Les points (M1,M2,M3) sur Q et (M1',M2',M3') sur Q' ont les coordonnées projectives:

M1 (0,0,1), M2 (0,1,0) M3 (1,0,0)
M1'(0,0,1), M2'(0,1,0) M3'(1,0,0)
Première propriété de H:
H(M1') = M1, H(M2')=M2, H(M3')=M3
H(0,0,1)=(0,0,1), H(0,1,0)=(0,1,0), H(1,0,0)=(1,0,0)
L'homographie H est donc réduite à la matrice:

| a 0 0 |
H=| 0 b 0 |
| 0 0 c |

avec a.b.c différent de 0.

Tous les points de Q et Q' sont exprimés en coordonnées projectives avec leur matrice respective.

Seconde propriété de H:

Pour les points Pi qui n'appartiennent par au VIP, le transformé Mi"=H(Mi') est aligné avec la droite {Mi,E} sur Q. Ces points sont appelés points secondaires. L'alignement {Mi,Mi",E} avec l'épipôle E (Xe,Ye,Ze) donne l'équation:

Equ.1: Alignement des points homologues avec l'épipôle

Soit:

Xe[c.Yi.Zi'- b.Zi.Yi'] - Ye[c.Xi.Zi' - a.Zi.Xi'] + Ze[b.Xi.Yi' - a.Yi.Xi'] = 0

Nous éliminons les coordonnées de E pour obtenir une meilleure stabilité. Pour chaque équation, nous prenons trois couples de points secondaires d'indices i,j,k (différents entre eux et supérieurs à 3 pour ne pas utiliser les points de base qui sont confondus par définition), ce qui donne le nouveau système d'équations:

Equ.2: Système d'équations des coefficients de l'homographie

Avec n points, nous construisons C(n,3) équations de ce type, qui correspondent à un système d'équations avec les variables liées a, b, c:

A.b/c + A'.c/b + B.c/a + B'.a/c + C.a/b + C'.b/a + D = 0

Equ.3: Equation des coefficients de l'homographie

Dans lequel les variables liées peuvent s'écrire:
xa=b/c, xa'=c/b, xb=c/a, xb'=a/c, xc=a/b, xc'=b/a,
soit:

A.xa + A'.xa' + B.xb + B'.xb' + C.xc + C'.xc' + D = 0

Système linéaire à six inconnues

Avec xa.xa' = xb.xb' = xc.xc' = 1

Nous résolvons le système par la méthode des moindres carrés et nous obtenons deux autocontrôles:
- Le résidu des moindres carrés LSQ du système à C(n,3) équations
- L'erreur de cohérence des variables liées qui doivent respecter la contrainte xa.xa' = xb.xb' = xc.xc' = 1, notée ERRCOEF.
Ces deux valeurs sont faibles si les points respectent la contrainte épipoplaire. Elles nous renseignent donc sur la qualité de l'appariement des points entre les deux images.
Nous calculons une solution avec 8 couples de points qui forment
3 paires de points de base définissant le plan virtuel VIP
5 paires de points secondaires qui forment C(5,3) = 10 équations linéaires
Comme les coefficients a,b,c sont calculés à un facteur près (espace projectif), nous fixons c=1 et obtenons les coefficients a, b ainsi que les autocontrôles décrits ci-dessus. Nous calculons les épipôles E et E' qui ont les mêmes coordonnées projectives en reprenant l'équation 1.
Cette résolution nous permet de recalculer l'image homologue et de la superposer avec l'image de référence Q. Les couples de points de base sont superposés et les couples de points secondaires alignés avec l'épipôle. Toutes les images Mi,Mi" des points Pi appartenant au VIP sont confondues, et les autres sont alignées avec l'épipôle. Les droites épipolaires homologues sont superposées, nous avons résolu le problème de la géométrie épipolaire.
Les cas de dégénérescence se présentent:
- lorsque les trois points de base sont alignés, dans ce cas la base projective est dégénérée et le VIP n'est pas défini. il est donc impossible de résoudre le système d'équation pour calculer l'épipôle.
- lorsque tous les points appartiennent au VIP, dans ce cas les points Mi et Mi" sont confondu sur Q et ne permettent pas de calculer l'épipôle. Notons cependant qu'il fournit des droites conjuguées passant par le même point.

3.2 Résultats

Nous avons utilisé notre méthode sur différents types d'images et nous présentons un exemple de solution avec deux images d'une pyramide. Les points de base qui définissent le VIP sont pris sur la base de la pyramide, et l'on peut observer la transformation de l'image homologue par l'homographie calculée. Tous les points de la base de la pyramide sont confondus et la disparité entre les autre points homologues Mi,Mi" est fonction de l'altitude du point Pi par rapport au VIP et de la distance de Pi avec la caméra.

Image de référence (1)	Image homologue (2)
Image homologue transformée (3)	Superposition de (1) et (3)

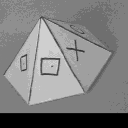
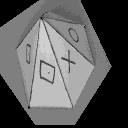
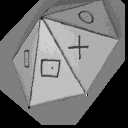
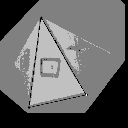
Dans les figures suivantes, nous présentons l'influence du choix des points de base sur le recalcul de l'image homologue. Pour chaque cas, les points de base correspondent aux sommets du triangle dessiné sur la superposition des images de référence et homologue recalculée. Les quatre exemples différents de position du VIP dans l'espace montrent la variation de la disparité entre les points Mi et Mi" en fonction de la distance (Pi - VIP). Notons que pour le troisième exemple, la mise en correspondance à l'intérieur du triangle défini par les points de base est réalisée puisque le VIP correspond à une facette de la pyramide.





Image de référence (1)	Image homol.transf.(2)	Superposition de (1) et (2)

Exemple de quatre différents recalculs d'images avec des points de base différents

4. Projection sur le VIP et calcul de C et C'

4.1 Modèle sténopé

Les éléments que nous utilisons dans cette seconde étape sont présentés dans la figure 4. Nous utilisons les coordonnées 3D de cinq points non coplanaires Pi ainsi que leurs images Mi et Mi" sur Q.

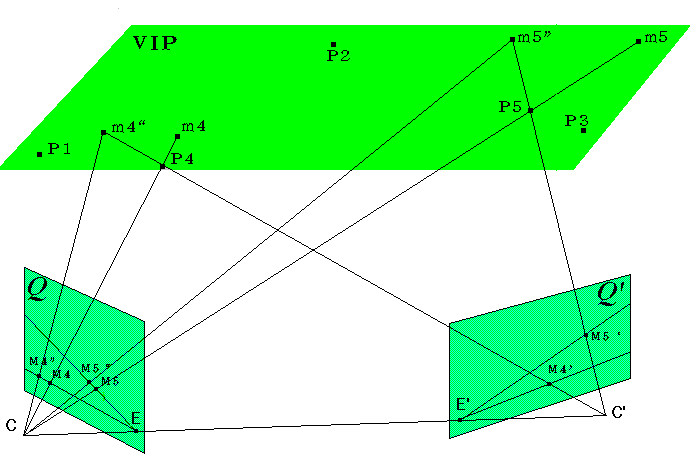
Fig.4: Alignement des points dans l'espace

Pour nous ramener au cas simplifié de stéréovision présenté dans le chapitre 2 de cet article, nous devons projeter le plan image Q sur le VIP et calculer les coordonnées des centres de projection C et C'.

Nous utilisons les images {M1,M2,M3} et {M1',M2',M3'} des points 3D {P1,P2,P3} comme repère projectif sur Q et Q' avec pour point unitaire le centre de gravité respectif de chaque triplet, comme dans le chapitre précédent. Puisque nous avons calculé l'homographie H entre Q et Q' correspondant à cette double projection utilisant le VIP, nous pouvons transformer les coordonnées de Q' en coordonnées H(Q') sur Q. Nous n'avons plus qu'une seule projection à réaliser de Q sur VIP par C.

Si nous considérons les points {P1,P2,P3,P4,P5} supposés connus comme base projective R dans l'espace, les coordonnées projectives des points sont:
P1 (1,0,0,0), P2 (0,1,0,0) P3 (0,0,1,0) P4 (0,0,0,1) P5 (1,1,1,1) et un point Pi dans R a pour coordonnées Pi(Xi,Yi,Zi,Ti).

Le plan virtuel VIP est défini par les trois points (P1,P2,P3). L'équation de ce plan est T=0 et la projection H1 de Q sur le VIP est définie par une homographie à deux paramètres u et v comme pour Q et Q'. Nous devons aussi calculer les coordonnées des centre de projection que nous pouvons écrire C: (Xc,Yc,Zc,1) et C': (Xc',Yc',Zc',1). Nous avons donc au total 8 inconnues à calculer pour définir la projection de Q sur le VIP et les coordonnées projectives de C et C' dans le référentiel R.

Les projections H1 de {M1,M2,M3,M4,M5} et {M1",M2",M3",M4",M5"} sur le VIP ont pour coordonnées m1=m1"(1,0,0,0), m2=m2"(0,1,0,0), m3=m3"(0,0,1,0), m4(u.x4,v.y4,z4,0), m4"(u.x4",v.y4",z4,0), m5(u.x5,v.y5,z5,0), m5"(u.x5",v.y5",z5",0) dans R.

Les contraintes utilisées sont les alignements des points (m4,P4,C), (m4",P4,C'), (m5,P5,C) et (m5",P5,C'). Chaque droite ainsi définie dans l'espace projectif R peut se décrire par l'intersection de deux plans, c'est à dire deux équations

Nous obtenons donc un système de 8 équations à 8 inconnues qui nous donne une solution unique qui définit la projection H1 de Q sur le VIP par C ainsi que les coordonnées projectives de C et C'.

Après recalcul de l'image homologue Q' sur Q par H, nous avons ainsi un moyen simple de calculer les coordonnées projectives d'un point P inconnu en utilisant les coordonnées projectives de ses deux images M et M" sur Q. Il suffit de transformer les coordonnées en m=H1(M), m"=H1(M"), puis de calculer l'intersection dans R des droites (C,m) et (C',m"). Le résultat nous donne les coordonnées projectives de P. Les coordonnées cartésiennes sont obtenues par l'application d'une matrice (4x4) coordonnées projective -> cartésiennes sur les coordonnées projectives de P.

Nous avons ramené le problème général de la stéréovision au cas particulier présenté au début du chapitre 2. Nous pouvons calculer le positionnement relatif des points dans un espace projectif si le coordonnées 3D des 5 points formant le référentiel projectif sont inconnues, et nous obtenons les coordonnées cartésiennes si les 5 points sont connus dans l'espace. L'utilisation des coordonnées 3D est reporté à la fin des calculs, ce qui évite la propagation des erreurs d'approximation des points dans l'espace.

4.2 Solution simplifiée pour la projection parallèle

La projection parallèle est un cas simplifié de modèle sténopé car les centres de projection C et C' sont rejetés à l'infini, ainsi que les épipôles E et E'. Il ne faut donc calculer que les directions de projection sur Q et Q'. Il suffit donc de quatre points non coplanaires dans l'espace pour résoudre le problème. La position dans l'espace d'un points P est obtenue en calculant l'intersection des deux parallèle à (m4,P4) et (m4",P4) passant respectivement par m et m' comme le montre la figure 5. On retrouve ainsi le résultat de Koenderink et Van Doorn sur les caméras affines [KOEN89].

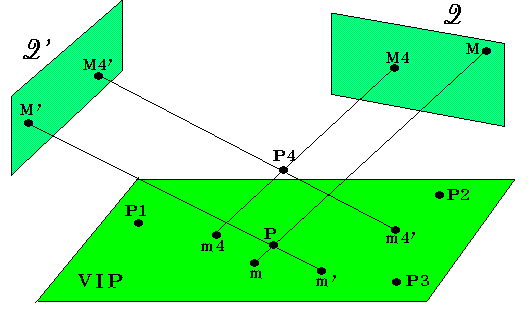
Fig.5: Relations dans l'espace avec la projection parallèle

Dans ce cas particulier, nous n'avons pas besoin de calculer la double projection de Q' sur Q, nous convertissons les coordonnées images en coordonnées barycentriques par rapport aux points {M1,M2,M3} pour Q et {M1',M2',M3'} pour Q'. Ensuite, nous revenons aux coordonnées cartésiennes par rapport aux points {P1,P2,P3} sur le VIP.

|x| |x1 x2 x3| |X|
|y|=|y1 y2 y3|*|Y|
|1| | 1 .1 .1| |Z|

Passage en coordonnées barycentriques

Méthode de calcul

1) Transformation des coordonnées images en coordonnées barycentriques par rapport à {M1,M2,M3} pour les points Mi sur Q, et par rapport à {M1',M2',M3'} pour les points Mi' sur Q'.
2) Transformation des coordonnées barycentriques des points Mi et Mi' en coordonnées cartésiennes mi and mi' sur le VIP par rapport à {P1,P2,P3,P4}.
Le points de l'espace P4 et ses images sur le VIP sont connues, donc (m4,P4) et (m4',P4) définissent les deux directions des projections parallèles.
3) Tout point P est calculé par l'intersection des parallèles à (m4,P4) et (m4',P4) passant respectivement par m et m'.

4.3 Expérimentation sur l'exemple pyramide

Nous avons testé les deux méthodes de calcul sur différents objets et nous présentons ci-dessous les résultats obtenus sur l'exemple pyramide. Trois sources d'erreurs perturbent l'évaluation des points dans l'espace:
1) La camera n'est pas un vrai modèle sténopé et les plans images présentent des distorsions.
2) La position des points homologues sur les images peuvent subir des erreurs d'évaluation allant jusqu'à trois pixels.
3) Les points 3D ont été mesurés à la règle et peuvent comporter des erreurs d'approximation.
Le but de cet expérimentation n'est pas d'obtenir la meilleure précision possible, mais d'évaluer l'intérêt de notre méthode de calcul dans de conditions courantes d'utilisation
La profondeur de l'objet est d'environ 10 cm et la caméra est située à environs un mètre de l'objet. Le tableau 1 présente la position des points mesurés sur les images (X,Y), (X',Y') et sur l'objet (X3D,Y3D,Z3D).

X	Y	X'	Y'	X3D	Y3D	Z3D
15	150	89	41	0	0	0
454	106	395	186	5	8.8	0
343	188	169	202	7.5	4.4	0
164	34	255	26	2.5	4.4	5
93	128	121	61	2.5	1.1	1.9
306	100	272	126	4.8	5.8	2.1
336	50	457	97	0	8.8	0
112	213	16	124	5	0	0
206	133	157	111	4.7	3.2	2
312	58	370	96	2.1	7.2	1.9

Table 1: Coordonnées des points sur les images et sur l'objet

La première étape de calcul pour la double projection de Q' sur Q par le VIP donne:
Homographie correspondant à la composition des deux projections: a=0.997 b=0.986 c=1 LSQ=0 ERRCOEF=0.03
Position des epipôles sur Q et Q': E=(1860, -1177) E'=(1573, -922)
L'erreur des moindres carrés LSQ et l'erreur sur les coefficients ERRCOEF est faible et valide le choix des points homologues sur les images, nous pouvons appliquer la deuxième étape du calcul.
Les tableaux 1 et 2 présentent les résultats obtenus pour le calcul des points dans l'espace avec le modèle sténopé et la projection parallèle. Chaque ligne d'un tableau présente la position d'un point mesuré sur l'objet (Xréel,Yréel,Zréel) (qui correspond au point du tableau 1), le point calculé (Xcalc,Ycalc,Zcalc), l'erreur des moindres carrés LSQ issue de l'intersection des deux droites dans l'espace (4 équations et 3 variables) ainsi que la distance entre le point mesuré et le point calculé.

Xreal	Yreal	Zreal	Xcalc	Ycalc	Zcalc	LSQ	dist.
0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00
5.00	8.80	0.00	5.00	8.80	0.00	0.00	0.00
7.50	4.40	0.00	7.50	4.40	0.00	0.00	0.00
2.10	7.20	1.90	2.10	7.20	1.90	0.00	0.00
2.50	4.40	5.00	2.50	4.40	5.00	0.00	0.00
2.50	1.10	1.90	2.52	1.53	1.82	18.21	0.44
4.80	5.80	2.10	4.90	5.70	2.17	17.08	0.16
0.00	8.80	0.00	-0.94	8.72	-0.29	1.07	0.99
5.00	0.00	0.00	4.42	0.12	-0.48	3.61	0.76
4.70	3.20	2.00	5.00	3.17	2.07	41.42	0.31

Table 2: Résultats des calculs avec le modèle sténopé

Homographie entre l'image Q et le VIP: u=0.0174 v=0.0183 w=0.017
Position des centres de projection: C=(50,5, -5.9, 37.9) C'=(79.9, 26.3, 80.7)
Somme des distances entre les points mesurés et les points calculés: 2.6 cm, soit une erreur moyenne de 2,6 mm.

Xreal	Yreal	Zreal	Xcalc	Ycalc	Zcalc	LSQ	dist.
0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00
5.00	8.80	0.00	5.00	8.80	0.00	0.00	0.00
7.50	4.40	0.00	7.50	4.40	0.00	0.00	0.00
2.10	7.20	1.90	2.10	7.20	1.90	0.00	0.00
2.50	4.40	5.00	1.80	4.32	5.10	0.03	0.71
2.50	1.10	1.90	2.08	1.38	1.80	0.02	0.51
4.80	5.80	2.10	4.52	5.72	2.16	0.00	0.30
0.00	8.80	0.00	0.00	8.54	-0.06	0.00	0.27
5.00	0.00	0.00	4.44	-0.14	-0.46	0.03	0.74
4.70	3.20	2.00	4.54	3.04	2.09	0.02	0.24

Table 3: Résultats des calculs pour la projection parallèle

Distance totale entre les points mesurés et les points calculés: 2.7 cm. Ce qui correspond à une erreur moyenne de 2,7 mm.
Les tableau 2 et 3 présentent les résultats pour les deux modèles de projection sur le même couple d'images stéréoscopiques. La reconstruction des points est presque identique. Ceci est dû au fait que si l'objet est compact et observé d'une distance suffisamment grande (plus de dix fois la profondeur le l'objet), alors il est possible d'approximer la projection par une projection parallèle sans trop d'erreur. Les avantages du modèle parallèle sont une meilleure stabilité que le modèle sténopé, ainsi que l'utilisation de quatre points de la scène au lieu de cinq.
La position calculée des centres de projection pour le modèle sténopé est aberrante, bien que la reconstruction soit acceptable puisque l'erreur de positionnement est de l'ordre de 3% par rapport à la taille de l'objet. Ceci pose le problème de la stabilité de notre méthode de reconstruction, qui pourrait être améliorée par l'utilisation d'un nombre plus important de points de la scène et l'utilisation de modèles de déformation pour les plans images.

5. Conclusion

La méthode de reconstruction d'une scène tridimensionnelle par projection sur un plan virtuel de l'espace présente plusieurs avantages:
- Le calcul de la géométrie épipolaire nous donne des autocontrôles sur la validité du choix des points homologues sur l'image.
- La reconstruction des points 3D peut être obtenue en connaissant la position de 5 points de la scène dans le cas du modèle sténopé, et 4 points pour la projection parallèle. Si les points de la scène sont inconnus, il est tout de même possible de calculer le positionnement relatif des points dans l'espace comme dans d'autres méthodes [SHAS93] [FAUG92] [LUON92].
- Le recalcul de l'image homologue par rapport à l'image de référence est un premier pas vers la mise en correspondance. Son avantage est de représenter les deux images dans un même référentiel et de superposer tous les points correspondant au VIP dans l'espace. Cette transformation est utilisée en coopération avec un critère de ressemblance de forme entre contours, pour extraire automatiquement des points homologues sur les deux images. Cette technique sera présentée dans un prochain article qui est détaillé dans [COUA94].
- Cette approche permet aussi de calculer en 2D un modèle à facettes et présente l'avantage d'une évaluation simple des disparités puisque tous les points homologues sont confondus lorsque le VIP correspond à un plan de l'objet dans l'espace.
Le but principal de notre travail actuel est d'obtenir une meilleure stabilité en utilisant des modèles de déformation sur les plans images et en augmentant le nombre de points connus dans l'espace.

Remerciements

Je remercie Mr Eugene Duclos, professeur de mathématiques pour son aide au cours de ce travail

Bibliographie

1. [AYAC89] Ayache , Nicholas. Vision st,r,oscopique et perception multisensorielle. Inter ,ditions science informatique (1989).
2. [CARR71] Carr,, Jean. Lecture et exploitation des photographies a,riennes. Editions EYROLLES Paris (1971).
3. [CHAU89] Chaumette, Fran[daggerdbl]ois. R,alisation et calibration d'un syst[Sinvcircumflex]me exp,rimental de vision compos, d'une cam,ra mobile embarqu,e sur un robot manipulateur. Rapport de recherche INRIA Rennes nø994 Mars 1989
4. [COUA94] Couapel, Bernard. St,r,ovision par ordinateur, g,om,trie et exp,rimentation. Th[Sinvcircumflex]se en informatique, Univerist, de Rennes 1 (1994).
5. [DUDA70] Duda, Richard.O. HART, Peter E. Pattern classification and scene analysis. Artificial intelligence group. Stanford research institute Menlo Park California December 1970
6. [EFIM81] Efimov. G,om,trie sup,rieure. Traduction francaise, ,ditions Mir Moscou (1981).
7. [FAUG92] Faugeras, Olivier. What can be seen in three dimensions with an uncalibrated stereo rig ? Computer vision ECCV '92. Lecture notes in computer science 588. Springer Verlag (1992).
8. [FAN_91] Fan, Hong. Yuan, Baozong. An accurate and practical camera calibration system for 3D computer vision Chinese journal of elctronics, June 1991.
9. [HURA60] G,n,ral Hurault, L. L'examen st,r,oscopique des photographies a,riennes. Imprimerie de l'IGN Paris (1960).
10. [LONG81] Longuet - Higgins,H.C. A computer algorithm for reconstructing a scene from two projections. Nature Vol. 293, 10 september 1981.
11. [LUON92] Luong,Quang Tuan. Matrice fondamentale et calibration visuelle sur l'environnement. Th[Sinvcircumflex]se en informatique. Universit, de Paris Sud Centre d'Orsay (1992).
12. [MOHR92] Mohr, Roger., Morin, Luce. Geometric solutions to some 3D vision problems. LIFIA - IMAG Grenoble (1992).
13. [MOHR93] Mohr, Roger. Projective geometry and computer vision. Handbook of Pattern Recognition and Computer Vision. World Scientific Publishing Company (1993).
14. [MORI93] Morin, Luce. Quelques contributions des invariants projectifs ... la vision par ordinateur. Th[Sinvcircumflex]se en informatique. Institut National de Polytechnique de Grenoble (1993).
15. [SHAS93] Shashua, Amnon. Projective depth: a geometric invariant for 3D reconstruction from two perspective / orthographic views and for visual recognition. IEEE Feb. 1993

| Se connecter | Plan du site |

RSS 2.0